音の物理の基礎

本記事では、音の物理の基礎を学びます。

音の特徴を捉えるうえで非常に重要となる周波数特性の考え方について理解することができます。

音の正体

音とは、空気の振動です。

空気が振動すると、空気中に圧力が高い部分と圧力が低い部分が現れます。

上記図では、赤色が濃い部分が圧力が高い状態、赤色の薄い部分が圧力の低い部分を示しています。この圧力の分布が、空気中を伝搬し、我々の耳に到達し、鼓膜が振動することで、音として認知することができます。

この、音の圧力の分布の変化を、わかりやすいように波の形で表すと、下記の図のようになります。圧力が高いとプラス方向に、圧力が低いとマイナス方向に表記します。

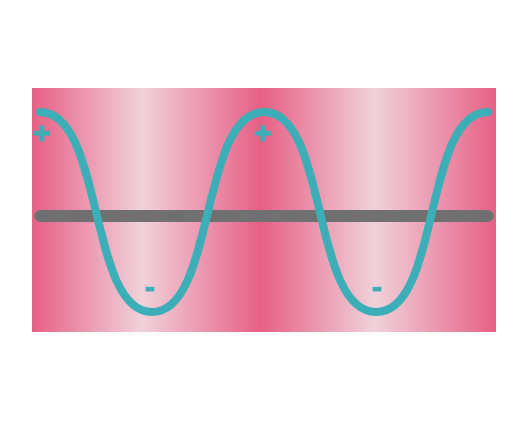
私たちがよくみる「音波の図」というのは、このように、空気の圧力変動を波の形で表したものになります。

実際の声で考えると、この空気の振動はもっと複雑なものになります。
以下は、声の空気振動をイメージした模式図です。

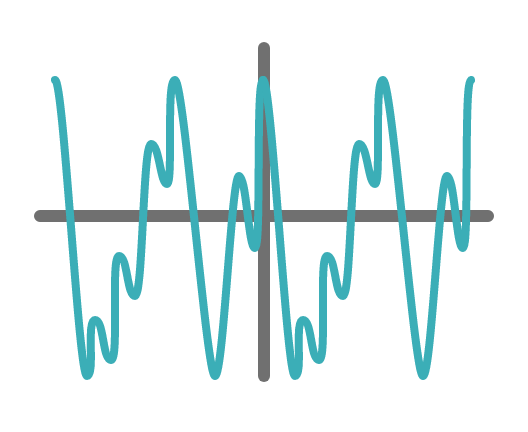
音を分解する

どんな複雑な波であっても、実は複数の単純な波(正弦波)を足し合わせることで再現することができます。

例えば、以下のような波があったとします。

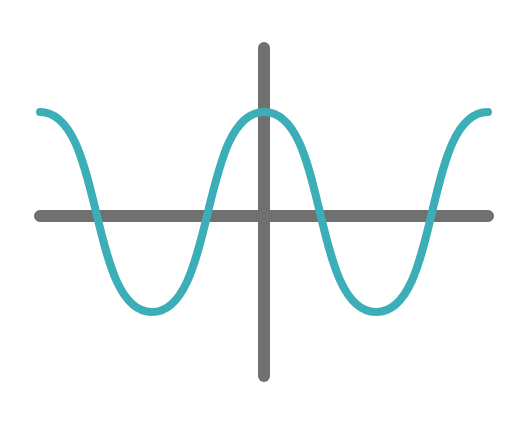
1秒間にA回、疎密を繰り返す、強い波(AHzの強い正弦波)

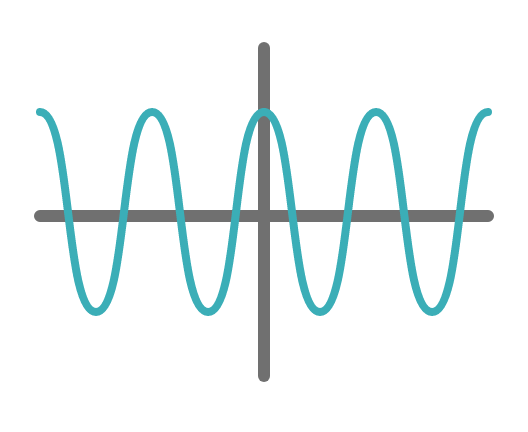
1秒間にB回、疎密を繰り返す、強い波(BHzの強い正弦波)

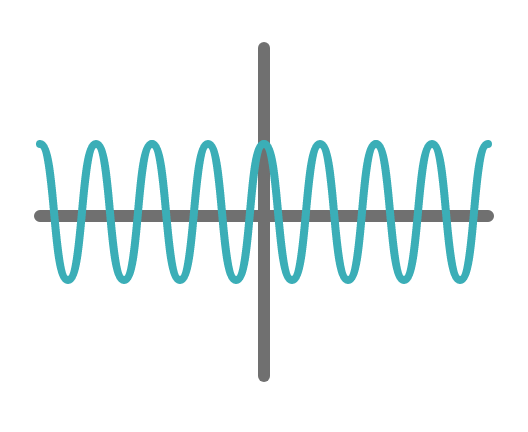
1秒間にC回、疎密を繰り返す、弱い波(CHzの弱い正弦波)

このような、シンプルな波をいくつも組み合わせていき、全て合成したとします。

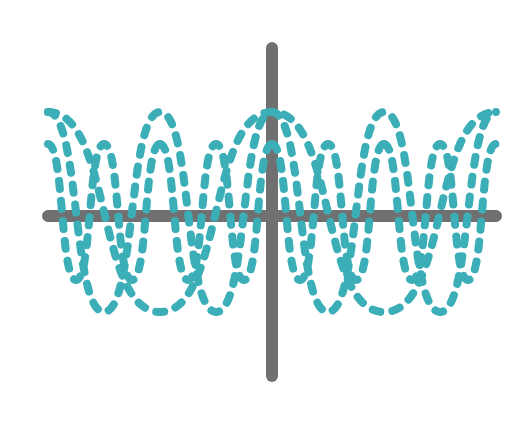
そうすることで、以下のような複雑な形の波であっても、作ることができます(下図はイメージです)。

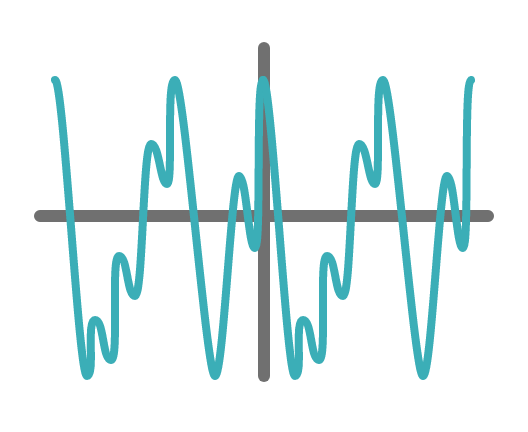
繰り返しになりますが、どのような音でも、正弦波の組み合わせにより表現することができるのです。

周波数特性とは

先ほど学んだ通り、どんな複雑な波も、単純な波の組み合わせで表現できます。

逆に考えると、どんな複雑な波であっても、単純な波に分解して考えることができる、ということです。

先ほどの例だと、波は以下の3つの波で構成されていました。

• AHzの強い正弦波
• BHzの強い正弦波
• CHzの弱い正弦波

では、今度はこれらを横軸を周波数、縦軸を強さとして、図に表現してみます。

すると、以下のようになります。

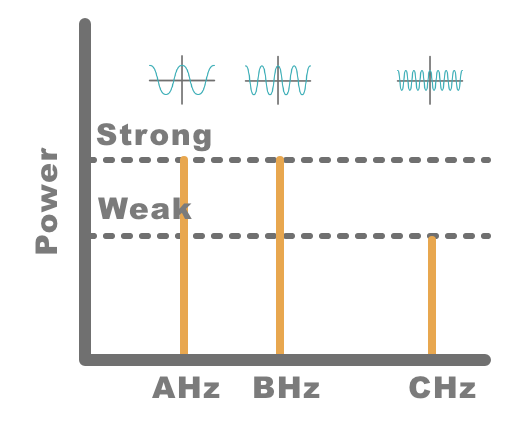
先ほどの複雑な波が、AHzの強い波と、BHzの強い波と、CHzの弱い波に分解できることを、一つの図の中に示しています。

まさにこの図のことを、音の周波数特性と呼びます。

つまり、音の周波数特性とは、その音がどのような構成で出来上がっているか(どれくらいのパワーの、どれくらいの周波数の正弦波の組み合わせでできているのか)を示す、いわば音の設計図ということができます。

本記事では、極力わかりやすくなるように、音についてシンプル化して説明しましたが、実際は、声の周波数特性は以下のような形になります。

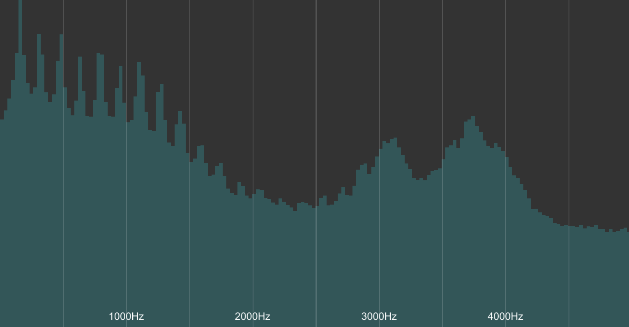
200Hzほどの波の成分を強く持ち、さらに3000Hz〜4000Hzの波の成分も強く含む声だということがわかります。

周波数特性の考え方を理解できれば、声についてより深い理解ができるようになります。音の概念、周波数特性の概念をしっかりと掴んでいきましょう。

本記事のポイント

• 音は、空気の振動
• 音波は、空気の圧力の高低を示したもの
• どんな複雑な波も、シンプルな波に分解することができる
• 周波数特性(スペクトル)とは、音の設計図のこと

最高のボイストレーニングアプリをあなたのポケットに

ボイストレーニングアプリ「Voick」を使えば、自分の歌声の分析を行いながら、ボイストレーニングを行うことができます。音声解析技術を用いた、新しいボイストレーニングの形を、是非ご体験ください。

Voickで
自由な歌声を獲得しましょう